CHAPTER TWENTY-SIX
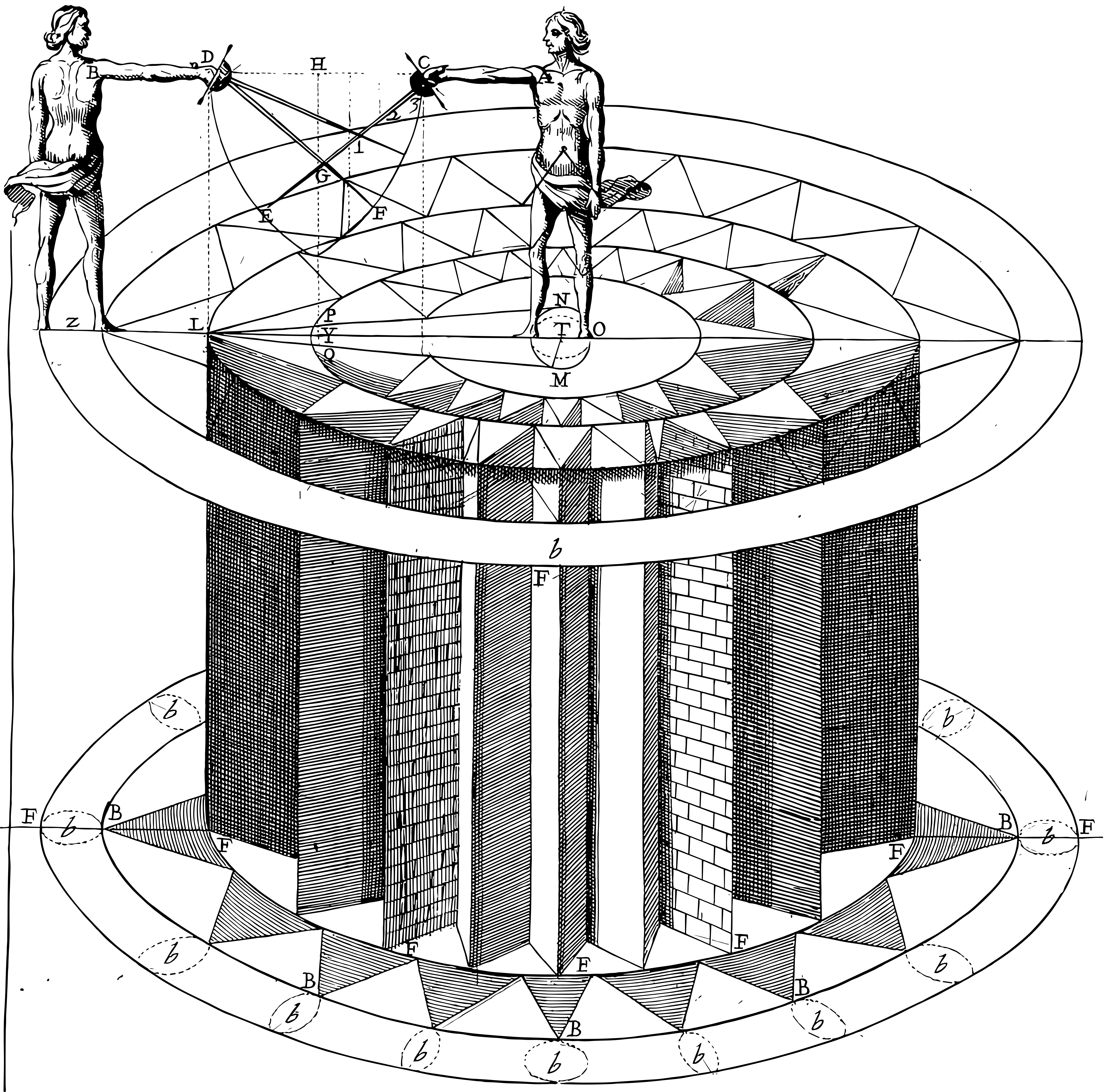
Demonstration in which the method by which the Fencer will have the Angles of the bastions of the idea of our Fort is manifested, which consists of containing the sword of his opponent in two vertical planes, touching on both sides of the cylinder in which we imagine the Fencer, or others with a larger diameter than the base requires; and the intersection of these planes is considered along a perpendicular line that falls from the center of the quillons of the guard of the opponent’s sword to the lower plane, wherever it may be located; and this perpendicular line we imagine produced up to the horizontal plane, which passes through the verticals of the two combatants: and because this demonstration has some cases, they will be explained in their order with their figures.
First, in dealing with the demonstration of this proposition, it is necessary for the Fencer to understand that his opponent cannot attempt to offend him, except through one of the three Angles - straight, obtuse, and acute - and through the jurisdiction of each one of them, which we have defined; in whose jurisdictions are included all the postures and operations that a man can perform with the sword in hand.
The Fencer places his Sword with the motion of the center C. of his hilt in an acute angle, describing the arc D.E. with the tip of the Sword, causing a semirect angle with the line C.D. part of the common section of the primary vertical plane with the superior plane, cutting the line of the opponent’s Sword D.F. at point G. in equal degrees, resulting in having equal power; in this position, it is recognized that the tip of the opponent’s Sword does not have direction to the body of the Fencer.
I say that from this position the opponent will not be able to make an immediate movement to hurt, without the Fencer being able to make another, or others at the same time for his defense, even though he makes it with at least ten times the speed, as will be demonstrated; although there may be many, due to the possibility of the opponent directing his Sword in the jurisdiction of the acute angle to different points of contact on the Fencer’s body, for clarity, we will reduce them to three, because once these are understood, the others will be understood as well.
Given, then, that the opponent raises his Sword from point G. to point 1. to hurt, in which action it is necessary that he puts degrees of lesser force into others of greater force than those of the Fencer; it is necessary to ascertain, what amount of movement does the Fencer make to place his opponent’s Sword in either of the two vertical planes that constitute the imaginary bastion of his Fortress?
We say that the equal distances Y.P. and Y.Q. determine the movement that the Fencer, positioned at the first section point, must make with the opponent’s sword to move it from the primary vertical plane to his right or left side, so that his sword passes over the surface of the bastion M.L.N., ensuring his defense, as clearly seen in the figure, without further demonstration.
However, for clearer understanding, we will examine it in this way: Draw from point T, the center of the Fencer’s cylinder, the line T.M. to the point of contact, which will be perpendicular to it by proposition eighteen of book three of Euclid’s Elements, forming the triangle L.T.M., similar to the triangle L.Y.Q., as they are subcontrary sections and both equiangular, since angle T.M.L. (right) is equal to angle L.Y.Q., and angle L is common, and the remaining angle T is equal to angle Q. Thus, their corresponding sides are proportional, and as L.T. is to T.M., so is L.Y. to Y.Q. Given the negligible difference between L.Q. and L.Y., to avoid fractions, we take L.Y. instead of L.Q. Thus, of these four quantities or sides, being three known, the fourth Y.Q. will also be known, though it can be verified with a compass, which is the diameter line divided as said, for clarity we do it by numbers, using the rule of three, saying: If six feet and a quarter of another, which are 100 fingers, give us half a foot, T.M., which are eight fingers, what will L.Q. give us, two feet and a quarter, which make 36 fingers? It will be found that the line Y.Q. will be two fingers and 88 hundredths of another, which are about 3 fingers; and this is the amount of movement the Fencer must make with his sword to place the opponent’s sword tangent to his cylinder M.O.N.
From this demonstration follows the understanding of the great advantage the Fencer has over his opponent by utilizing the principle of movement, since to initiate an attack from the medium of proportion, the opponent needs to make a movement with the whole body, at least two feet and a quarter, which are 36 fingers, whereas the Fencer, in the position shown in the figure, with just a three-finger movement of the center of his wrist, causes the opponent’s sword to be unable to offend, producing the same effect as if he were actually behind the bastion, in which we imagine him, represented in its base L.P.q. In this case, not only does the Fencer have an advantage of at least ten to one, but even twelve to one, in terms of swiftness.
We say that the two lines L.M. and L.N., initially imagined as tangents to the base of the Fencer’s cylinder N.O.M. in the lower plane, which are the two sides of the larger triangle M.L.N. with vertex L. also common to the smaller triangle, whose sides are L.P. and L.Q. and its base P.Q., determines the plan of the Fencer’s bastion in its exterior polygon; and the line P.Q. and F.Q. determine the distance the Fencer must move his sword away from the primary vertical plane, on either side, to keep it on the surface of his cylinder.
We imagine that all this moves from the lower plane, and that the two sides of the larger triangle L.M. and L.N., without departing from the surface of the Fencer’s cylinder, and the vertex of angle L., rise equally, creating two vertical planes from the top of the Fencer’s head, always parallel to the horizon.
From this construction and this imaginary bastion, follows a true consequence: if the Fencer’s body is encompassed by the two vertical planes forming the angle of this bastion, and the opponent’s sword is outside them, no one can doubt that the Fencer will be defended; and having demonstrated in this first case the ease with which the Fencer can place the opponent’s sword in either of these two vertical planes, with swiftness and advantage in the short movements he makes, the purpose and great utility that results from the imagination of our Fort’s idea are proven, which in effects serves the Fencer any bastion of it, as if it were of dense material, as each one can experience, making use of what has been demonstrated and will be demonstrated in other cases.
Although in this and other propositions and figures related to the formation of the angles of the bastions of our Fort’s idea, we suppose that from the posture of the right angle, the swords descend to the acute angle with the movement of the wrist, to the extent that it seems they fall from the hand, since they cause a semi-right angle with the line of the upper right angle; the Fencer is advised that this has been done to calculate more accurately and ascertain the amounts of movements; thus, understand that in the operations of the battle, it is not necessary for the swords to descend so much into the acute angle, but only as much as necessary, as will be demonstrated in the parries and tricks of the third book.
Given the same as in the previous case, it is assumed that the opponent raises his sword from the first point to offend the Fencer, in a right angle, and when reaching the second point, the Fencer, making use of the greater degrees of strength of his sword, in the weaker degrees of the opponent’s, moves it to his left side with the movement of his wrist, so that it does not have direction towards his body; and to know how much movement he will have to make from this position to achieve it, avoiding the Geometric demonstration that we made to demonstrate the previous case, to avoid prolixity, given that it turns out to be the same demonstration, due to the similarity of the triangles.
We say by the rule of three, if the line L.T. of six feet and a quarter, which are one hundred fingers, gives me T.M. which is half a foot, which are eight fingers, what will L.5. of forty-four fingers give me? And it is found that the movement that the Fencer will have to make to place his sword against the opponent’s on the surface of his cylinder, will be three fingers and fifty-two hundredths, which are just over three and a half fingers: and if at the same time the opponent gives his step of two feet and a quarter, which are thirty-six fingers, to offend him, still the Fencer will have an advantage in swiftness, as of ten and two-sevenths to one.
For this third case, it is assumed that the opponent, from the second point, raises his sword to the guard of the Fencer’s sword at the third point, while simultaneously taking a step of two feet and a quarter to reach a contact point on the Fencer. When the opponent’s sword reaches the third point, the Fencer attempts to defend and move it in such a way that he cannot be struck; it is necessary to examine the amount of movement he must make from this position to his left. As in the previous two cases, we rely solely on the rule of three.
We say, if L.T. are six feet and a quarter, or one hundred fingers, and it gives me T.M. of half a foot, which are eight fingers, what will L.8. give me, which are three feet and a quarter, or fifty-two fingers? Performing the operation, it indicates the amounts marked 8. and 9., and it will be found that the movement the Fencer must make with his sword to place the opponent’s from this position on the surface of his cylinder will be four fingers and 16 hundredths, which are just under four and an eighth, at the time when the opponent takes his step of two feet and a quarter, which are thirty-six fingers, giving the Fencer an advantage of eight and three-fifths of a finger to one; and this advantage that the Fencer has over his opponent is greater than what is usually given by the Military to any of those defending the Royal Fortresses against the besiegers, which is about six to one, although some authors give it as ten to one. This means that one of those in the Fortress is worth six of those outside attacking.
The same calculations made in the three cases mentioned also apply if the Fencer places his sword on the outside of the opponent’s, to carry it with his own to his right side, moving it away from the vertical plane. In this same order, all other positions can be calculated, whether on the inside or outside, in which it will always be verified that the Fencer has a significant advantage over his opponent, and that at least, as said, he will have an advantage of eight to one, enjoying only the beginnings of the movements, in the way that has been noted.
In the three preceding cases, it has been demonstrated that, when the opponent attacks the Fencer intending to strike with a thrust, and the swords are in the acute angle on the left side, and on the right, the amount of movement that the Fencer must make for his defense is established. This is done by placing his sword on the opponent’s, within the two vertical planes formed by his bulwark, thereby ensuring his defense.
To recognize the defense that the Fencer also has in any other situation, I assume the same three cases in the obtuse angle. Since the same rules apply to their examination as in the previous three cases, without any difference, and our intention is to avoid repeating what can be understood from what has already been said, we refer to them. However, to satisfy, we will explain them in the following manner.
Given the same conditions as in the previous cases, except that in those, the swords are in an acute angle, and in these, it is assumed to be an obtuse angle, with the same divisions from point G. to 1.2.3. &c., as shown in the following plate. Thus, the demonstrations we made in the previous cases also apply without difference to the cases of the obtuse angle, because the Fencer will make the same amounts of movements on both sides, at the time the opponent moves his body or the cylinder we imagine it in, as demonstrated. Therefore, we avoid the demonstrations of the other cases to not repeat them, since drawing their perpendiculars from the points of the divisions on the lower plane will cut the plant of the bulwark, imagined for the Fencer’s defense, causing the same similar triangles, with their corresponding sides, in the same way they were caused, and the plant of this bulwark, from the divisions, in the types of figures passed, with both opponents affirmed with them in the jurisdiction of the acute angle. It concludes that there is no essential reason for difference from the cases of the acute angle to those of the obtuse angle, and that the defenses the Fencer has in the former are of the same quality in all respects as the defenses he has in the latter.
In what we have demonstrated about the concept of our Fort, it has been mentioned how with short amounts of movements the Fencer will defend himself with his sword at the time his opponent wishes to offend him with a thrust in any of the jurisdictions of the 3 angles, assuming a compass movement of two feet and a quarter, and the advantages he will gain, regulated by the amount of his opponent’s compass and by the movements of his sword, so that the opponent’s sword does not have a direction towards his body. Now, it is appropriate to demonstrate how the Fencer gains many greater advantages in any of these cases. For this purpose, we assume as a constant that at the time the opponent gives the referred compass movement to strike, the Fencer can simultaneously make a revolution or Pyramid with the center of the wrist; in such a way that the actions of both end at the same time, considering that it is even easier and quicker for a part to move than its whole, as anyone can experience, and we have asked this to be acknowledged by petition. Given the possibility of this equality between the two opponents, we will prove this greater advantage in the fifth case, whose understanding will serve for the others that remain explained.
We imagine that having moved the opponent’s sword from point G to I, it has entered the jurisdiction of the Fencer’s defensive Pyramid, in which it has greater degrees of strength and power, to place the opponent’s sword in its vertical plane of defense (side of its bulwark) and the surface of its cylinder, by simply making point I of the intersection of the swords move to its left side by an amount of three fingers; and to know the proportion these three fingers have with the amount of movement that can be made in the entire revolution of this point I, or defensive Pyramid with the semidiameter I.K, we will describe the circle X.Q.I.P. and it will be the base of this Pyramid C.I.X., with I.X. as its diameter; take I.P.I.Q. on both sides of the diameter I.X. equal to I.P.I.Q. that are on the plan of the bulwark P.L.Q., each one of them, as we have said, is three fingers; and by the same figure mechanically, it can be found, more or less, how many times this smaller portion of I.P. enters the entire circumference of the circle, or base X.Q.I.P., which will be about 42 times, an advantage that the Fencer will have over its opponent; and the same is found by numbers, examining by the amount of the diameter I.X. which is two and a half feet, or 40 fingers, the circumference of the circle by Archimedes’ rule, saying: If seven give me 22, what will 40 give me? and the quotient will be 126 fingers, which will be the circumference of this circle: and dividing it by the three fingers, that the Fencer needs to make, so that the opponent’s sword does not have a direction to its body, and passes by the surface of its cylinder, it comes to 42, which proves that the advantage that the Fencer will have over its opponent, enjoying the beginning of the movement, when it gives its compass to strike it with a thrust of first intention, is like 42 to one.
Given, then, that it attacks the Fencer, as in the previous case, from the inside, to strike from the outside, in two ways the Fencer can make its defense; one will be, at the time it is attacked from the inside, to make from the primary vertical plane, where its sword has the amount of the three fingers of movement to its left side, as has been demonstrated, to remain defended; and attacking immediately to strike it from the outside, it will have to make from the same position an amount of six fingers of movement to its right side, to also remain defended: so that the Fencer will have made in these two actions an amount of nine fingers of movement, and having made the account in the referred order, it will be found that in the circumference of the circle, or base of the said Pyramid of 126 fingers, the advantage will be like 14 to 1.
Because the opponent can carry the intention of making three attacks, the first two being to dispose, and the third to return to execute from the inside: in this case, the Fencer to remain defended will have to make another amount of six fingers of movement to its left side, with which there will be fifteen fingers that the Fencer will have made in the three actions; and having made the account in the same order, it will still be found that it enters the circumference of the circle, or base of 126 fingers, eight times.
Since these calculations are adjusted strictly to the precise movements of the defense, and it is so that the acceleration of the attacks will often oblige the opponent many times to make the Fencer do more movement, on one side and the other, we advise the Fencer, for greater security, not to allow its opponent to attack it by the primary vertical plane of first intention, but when it lowers its sword to the acute angle, to gain the advantage of the first three fingers, immediately impeding the plane, on any side in which the opponent’s sword has direction to its body, to remain, without further diligence, defended, trying to have contact with the sword, to have knowledge of its movements; with which, not only will it have the aforementioned advantages, but also in these three actions of attack more advantage of three fingers, which it will not have to make of movement, from which the Fencer will follow another advantage, because by impeding its opponent’s planes immediately, it will oblige it to make a greater portion of Pyramid to offend, and the one it makes will be much smaller, and with more composure, because as these actions are repeated to the attacks, it causes some kind of more alteration, and in the greater portion of Pyramid that the opponent will make, the Fencer will have a supplement, when it makes by mistake, or by another accident, more than the six fingers of movement, on one side and the other, respecting what has been said: and they will always be, however this is examined, its greater advantages; and the Fencer immediately impeding the planes to its opponent, will be by means of our four universal modes, which are reduced to real or virtual blockages, as explained in their place.
The second mode with which the Fencer can make the same defenses, which we have explained, will be to immediately impede the planes of its opponent, also giving compass for defense, or offense, or both things together, as will be specified in the Treatise of the Tricks, and this way of working will be safer, and more immediate to offend.
With which we have explained the defenses that the Fencer has in the three angles, right, obtuse, and acute, when its opponent wants to offend it with a thrust; but as our intention is that the Fencer can perform its defenses and offenses universally, not only against thrusts, but also against vertical, diagonal cuts, and reverses of both species, and against cuts, and horizontal reverses, and half cuts, and half reverses of the species that can be formed, which are all the tricks of the possibility of man; and the one and the other necessarily have to be executed with natural, accidental, and reduction movements, and their mixtures.
Because in what has been demonstrated in the previous figures, only the accidental and natural movement has been dealt with, it is necessary, for this to have generality, that the Fencer is also given defense for the offensive movement. We say that the opponent, according to its possibility, can assert itself in one of two ways, and that each one of them is capable of different postures.
The first, can be asserted in different ways, so that its sword has direction to the body of the Fencer, both in the primary vertical plane and in other planes, and postures; and in all of them, keeping the Fencer to the precepts that have been demonstrated in said figures, it will be able to place the opponent’s sword in any of the two vertical planes of its defense, by means of its imaginary bulwark.
To ensure adherence to the aforementioned principles in fencing, a general rule is provided: whenever the opponent’s sword is directed towards one’s body, a vertical plane should be considered as the primary reference. This plane should pass through the opponent’s sword and the center of its cross-guard, as well as along the fencer’s directional line. Whether this plane passes through the fencer’s right side, aligns with the diametral line of the chest, or is positioned in any other affirmed manner, the fencer should always occupy this plane with their own sword and guard. This occupation should be similar to when both fencers are positioned at a right angle on the primary vertical plane, which is assumed to be a shared point of reference for both combatants. Just as the opponent places their sword on one of the vertical planes of defense, the fencer should do the same in any other plane where the opponent’s sword is directed towards their body. Even when the fencer’s sword positions the opponent’s within the vertical planes of defense, this specific plane should remain occupied by their guard, passing through the center of their cross-guard and that of the opponent’s, or by employing other precepts in all instances, as when they are positioned on the primary vertical plane.
Warning
Thus, the fencer will have two forms of defense: one by positioning the opponent’s sword within one of their vertical planes of defense, and another by occupying the aforementioned plane with their guard, preventing the opponent from attacking without passing through the jurisdiction of one of the pyramids demonstrated in previous cases. This approach requires the opponent to make significantly more movements than the fencer does to remain defended, often positioning them to attack the opponent.
The second method involves the opponent assuming any posture they wish, without their sword being directed at the fencer’s body. Whenever this happens, the fencer creates the necessary bulwark for their defense. By positioning their sword and body, the fencer can immediately block entry into their imaginary bulwark, striving to block other indirect and distant approaches the opponent might use to attack. This is achieved by positioning the fencer’s arm, guard, sword, and body in accordance with the principles of this science, which will be further clarified when discussing how the fencer can break down this Fort using various strategies: sometimes by making contact with the opponent’s sword, and other times without, depending on the posture and plane in which the opponent’s sword and arm are positioned.
For added security, the fencer can, through either contact or without, ensure that the opponent’s sword is kept further away from their own cylindrical space. Although the figures given have a diameter of one foot, which is necessary for defense, the fencer can choose to have the opponent’s sword further away to attack them in a different cylinder, possibly two feet in diameter or more, as best suits the situation. This can be easily achieved by considering, in any of the aforementioned postures, that the vertex of their outer bulwark corresponds to the center of the opponent’s cross-guard, and ensuring that the angle of the bulwark is greater than necessary, since the vertical planes of defense will be on either side of this angle, regardless of its formation.
Since this universality will be specified when discussing the formation of strategies, allowing the fencer to perfectly use this doctrine to form them, it is unnecessary to elaborate further here. With the information provided, the ease with which the fencer can form their defensive Fort and combine it with offense should be clear, as well as how they should conduct themselves in any situation, whether moving around the center or taking steps. In any case, they will always carry the concept of their Fort, considering the positions and postures of their body, arm, and sword in relation to the opponent’s, whether they are both in a proportionate middle ground, or if the opponent attempts to break the distance to attack. In this case, it is advised that if the fencer wishes to maintain a proportionate middle ground to use the bulwark of their external polygon, they can achieve this only by moving through the pyramid we consider in the strongest degrees of the sword, and the pyramid of the arm and guard. These two are especially useful when the opponent breaks the distance to attack; the two main ones are the arm and guard, and the entire sword, which includes the imagined pyramid in the strongest degrees. With these three pyramids, using them as required according to the precepts of this science, the fencer will find themselves in continuous defense during combat, ready to exploit immediate opportunities provided by the opponent, and those acquired for attacking.
However, it seems appropriate here to also discuss the advantages the fencer has with their sword for defending against their opponent when they attempt to strike, as demonstrated in previous cases and figures. We will also mention the advantages of moving the body around the center of the right foot within their particular circle, in opposition to the steps the opponent may take around the circumference of the circle of proportionate means, and also when the opponent attempts to enter.
It is assumed that the line of circumvallation A.E.B.D. is the plan of a Castle, Fortress, or jurisdiction of the means of proportion, whose center is C, and the small circle is the plan of the Fencer’s body, where he is affirmed on right angle, and in right angle with his Sword, and the center of his right foot at point C. It is also assumed that his opponent is also affirmed on right angle, and in right angle at point A, at a distance of eight feet from center to center of the right feet, and that being impeded the passage by the line A.C, he wants to attempt his assault through any of the sides A.F.A.H. Assuming that he gives a compass through the circumference of the means of proportion from point A to point F, draw the line F.C. to the center of the Fencer’s particular circle.
Because according to what was demonstrated by Archimedes, proposition three, all circumferences of circles have the same proportion as their Diameters; and so in this figure, the proportion that the semidiameter C.O. has to the circumference A.F.B. and permuting, will be like the semidiameter C.O. to the semidiameter C.A. the same has O.P.S. to A.F.B. and the part O.P. included in Angle A.C.F. to the part A.F. But by the same assumption, the semidiameter C.O. is one-eighth of the semidiameter C.A. then also the O.P. is one-eighth of the A.F. with which it is proven, that the advantage that the Fencer makes to his opponent, is as eight to one; this is understood by giving the semidiameter of the Fencer’s particular circle a Geometric foot.
But if it is given what Alberto says in his Symmetry, which is one-tenth of the height of the man, supposed to be six feet long, the advantage will be as nine and a half to one; and the same reason in proportion follows in everything if the opponent wants to give compass to hurt the Fencer from point A to point L, stepping on the orb of his Sword, if he gives compass to the middle of proportion at point H, or to the proportionate at point M, orb of the Fencer’s Sword.
From this, it results that if the opponent continues to give his compasses through the circle of the means of proportion, or wants to enter to hurt, giving compass from the distance of point A to point L, by moving the Fencer on the center of his particular circle, through the entire circumference of it, he will oblige his opponent with his compasses, in whatever part he will make the same advantage, opposing his bulwark; and according to these considerations, the Fencer will be found within his Fort, guarded by the bulwarks of his defense, as he will be in his possibility to place them in all the parts that are necessary in opposition to his opponent.